项泽亮教授团队在光力系统的量子相变理论研究中取得重要进展

       bet亚洲登录官方网站项泽亮教授团队最近在光力系统的量子相变理论研究中取得重要进展，解析验证了在经典极限下声子如何诱导光子在基态上实现凝聚。2024年1月30日，该成果以“Quantum Phase Transitions in Optomechanical Systems”为题，以bat365在线平台网站为第一单位发表在国际著名物理期刊《Physical Review Letters》。

      超辐射相变的概念最早起源于物理学家Klaus Hepp和Elliott H Lieb在1973年提出的一个二阶量子相变类型，描述了光子在基态上的凝聚现象。最初，此相变被预言可发生在由Dicke模型所描述的N个原子与腔模的相互作用系统。当N个原子在系统基态上处于高度相干时，腔内光子数在基态上表现为宏观占据，这就是超辐射相（光子凝聚）。此类相变本质上可通过朗道范式描述，即当原子数N趋于无穷时（即热力学极限），系统出现自发对称破缺且开始从一个平庸相转变到超辐射相。2015年，德国M.B.Plenio团队提出超辐射相变也可发生在由Rabi模型所描述的单原子与腔模的相互作用系统。他们解析证明在合适的系统参数，而非粒子数趋于无限时，系统也能够展现出相变的所有基本现象。这突破了传统认知，表明相变不一定要在热力学极限下才能发生，此结果随后获得量子模拟实验的验证。

图1：光力系统示意图

      通常来说，光子凝聚需要与自旋系统作用诱导才能产生，其相互作用本质上来源于库伦力和洛伦兹力。这很自然地引出一个问题，非自旋系统或者说不基于库伦力和洛伦兹力的量子系统，是否也可以得到超辐射相变？项泽亮教授团队的研究工作利用光力系统（optomechanical system）回应了这个问题。基于通过辐射压力相互作用的光力系统（见图1），他们解析证明了当系统参数达到经典极限，即光与振子的频率之比趋于无穷时，机械振动（声子）将诱导光子在基态上凝聚。

      此项工作中，研究团队发现了光力系统具有U(1)对称和Z₂对称这两种情况。当系统处于U(1)对称时，经典极限下，解析结果展示了基态附近的能级交叉[图2 (a)]以及光子在基态上占据分布[图2 (b)]。平均场理论也给出了一致结果，并进一步揭示该系统可激发Goldstone mode [图2 (c-d)] 以及临界点是一个二级相变点[图2 (e-f)]。

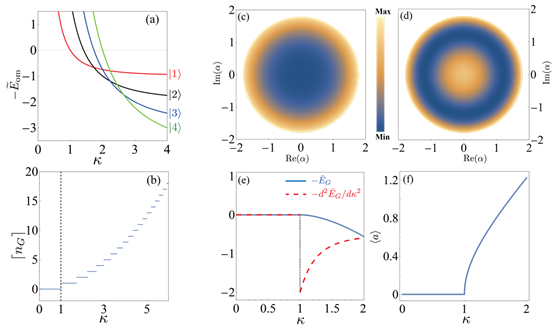
图2:（a）低能态在基态附近的能级交叉；（b）光子在基态上的占据分布；（c）平凡量子相在基态上的相空间分布;（d）超辐射相的相空间分布;（e）基态能量及其二阶偏导在相变点的连续性情况;（f）序参量分布。

      当系统处于Z₂对称时，利用变分原理和平均场可得出基态是一个同时拥有机械与光学模式压缩真空态的结论，并确定了超辐射相。有趣的是，利用压缩光驱动此系统，超辐射相所在区域可通过调节压缩振幅来改变。这一独特性质让研究者可以设计感兴趣的量子相图，达到研究不同非平凡相之间可能存在奇异临界点的目的。另外，他们还发现通过选择合适的压缩方向，系统相变所需耦合强度将会以指数方式大幅降低，极大地减少实验难度。最后，研究团队考虑了机械振子和原子同时与光场的相互作用系统。所得到的解析结果表明此混合系统将经过一个混合临界点后发生超辐射相变。该混合临界点的数学形式非常简洁，仅由光力系统和光-原子临界耦合强度共同组成，体现了它们的相互独立性。这个特点本质是因为系统拥有不同的相互作用（辐射压力与Dicke模型的库伦力和洛伦兹力），触发相变不一样的极限条件（经典极限和热力学极限），以及不同的对称性。根据这个结果，研究团队很快联想到如果这两个子系统所对应的非平凡量子相处于相邻位置，那么其边界点是否可能为退紧闭临界点，并进行了展望。

       该研究成果于2024年1月30日发表于Physical Review Letters 132, 053601 (2024)。bat365博士后王博为论文第一作者，项泽亮教授为论文通讯作者，并与日本理化学研究所（RIKEN）和密西根大学安娜堡分校的Franco Nori教授合作完成。阴帅副教授和日本NICT研究员Sahel Ashhab给与了讨论和支持。上述工作得到国家自然科学基金、国家重点研发计划、博士后面上项目的大力支持。

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.053601